MULTIAXIAL
Für multiaxiale Berechnungen wird zusätzlich zu winLIFE BASIC das Modul winLIFE MULTIAXIAL benötigt.
Von der Bauteilbelastung zur örtlichen Beanspruchung
Für eine Lebensdauerberechnung ist die Kenntnis der örtlichen Beanspruchung (Spannung, Dehnung) eine entscheidende Voraussetzung. Dabei gibt es verschiedene Problemstellungen, die mit unterschiedlichen theoretischen Ansätzen behandelt werden müssen. Zum einen spielt die Art des zu untersuchenden Bauteils (starr, flexibel, Mehrköpersystem) eine Rolle, zum anderen die Art der Belastung.
Belastungen können als Last-Zeit-Verläufe (Zeitreihen), als Lastkollektive (Häufigkeit von Laststufen) oder als spektrale Dichte der Belastung über der Frequenz (Leistungsdichtespektrum) vorgegeben werden. Wann die entsprechenden Methoden anzuwenden sind, wird hier kurz erläutert.
|
Bauteil |
Belastung |
Lösungsmethode |
Schnittstellenmakros / |
|
Elastischer Körper
|
Zeitreihe | Superposition von FE-Einheitslastfällen durch entsprechende Skalierung der Last-Zeit-Funktionen |
FEMAP, ANSYS |
|
Lastkollektiv |
Superposition von FE-Einheitslastfällen durch entsprechende Skalierung der Last-Zeit-Funktionen |
FEMAP, ANSYS |
|
|
Leistungsdichtespektrum |
Random Fatigue: |
Berechnung möglich, doch erhebliche Vorarbeiten des Benutzers nötig. |
|
| Mehrkörpersystem mit elast. Teilkörpern, große Relativbewegungen, Trägheitskräfte |
Im FEM/MKS-System |
Transiente Analyse: Import der Spannungstensor-Zeitfunktion aus FEM/MKS Rechnung | FEMAP / ADINA, ABAQUS, MARC, NASTRAN, PERMAS, RecurDyn |
| Flexibler Körper, Bauteilschwingungen sind relevant. |
Die auf das Bauteil wirkende |
Modale Superposition: |
RecurDyn / FEMAP |
|
Transiente Analyse: Simulation der Dynamik im Zeitbereich im MKS/FEM-System und Import der Spannungstensor-Zeitfunktion |
FEMAP |
||
| Leistungsdichtespektrum | Random Fatigue: FEM-Random Analyse, Übernahme der RMS-Werte aus FEM und Erzeugung eines schädigungsgleichen Lastkollektivs |
Berechnung möglich, doch erhebliche Vorarbeiten des Benutzers nötig. PERMAS, NASTRAN |
Superposition von FE-Einheitslastfällen: Starrkörper unter dem Einfluss zeitveränderlicher Belastungen
Wird ein Starrkörper durch eine oder mehrere Belastungsgrößen (Kraft. Moment) beansprucht, so können die örtlich auftretenden Spannungen und Dehnungen durch Kombination der (gemessenen) Last-Zeit-Funktion mit statisch ermittelten Einheitslastfällen berechnet werden.
Die aus den Einheitslastfällen gewonnenen Spannungstensoren werden mit den gemessenen Last-Zeit-Funktionen skaliert und für jeden Zeitschritt superponiert. Das Ergebnis ist eine Spannungstensor-Zeit-Funktion, die als Grundlage für die Schadensakkumulationsrechnung dient. Dies Verfahren ist anwendbar, wenn die Verformungen des Körpers im Verhältnis zu seinen Abmessungen klein sind.
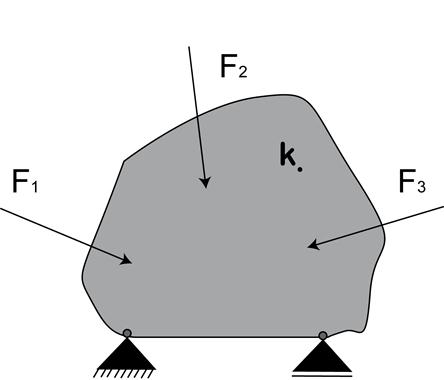
Für das Beispiel (Bild) wird daher benötigt:
- Der Verlauf der Kräfte als Funktion der Zeit (Zeitreihen): F1(t),F2(t),F3(t)
- Die Ergebnisse der zugehörigen FE-Einheitslastfälle.
Dabei wirkt jeweils eine Kraft FFE1, FFE2, FFE3 mit gleicher Wirkungslinie und gleichem Angriffspunkt wie die zugehörige Kraft. Das Ergebnis der FE-Berechnung sind die Spannungstensoren in jedem interessierenden Knoten (der Oberfläche) je Lastfall.
Nichtlineare, transiente Analyse: Veränderliche Bauteilgeometrie und zeit – und/oder richtungsveränderliche Belastung
Ändert ein Körper seine Geometrie sehr stark oder ändern sich die Richtungen der angreifenden Kräfte oder treten Trägheitskräfte auf, so ist die oben beschriebene Superpositionsmethode für die Berechnung nicht mehr geeignet. Als Beispiel sei ein Bagger (Bild) genannt, dessen Schaufel so bewegt wird, so dass sich die drei Winkel alfa, beta und gamma zeitlich verändern. Außerdem ändert sich die äußere Belastung durch die bewegte Ladung. In diesem Fall kann das Verhalten des Baggers durch eine MKS/FEM-Simulation berechnet werden. Dabei können für jeden Zeitpunkt die Kräfte und Spannungen an jedem interessierenden Punkt berechnet werden. Auch der Spannungstensor, der den Spannungszustand vollständig beschreibt, kann angegeben werden.
Exportiert man nun für die interessierenden Knoten k die Spannungstensoren für jeden Zeitschritt t, so kann darauf aufbauend eine Lebensdauerberechnung mit winLIFE durchgeführt werden. Auf diese Weise können auch andere geometrisch nichtlineare veränderliche Bauteile sowie Schwingungszustände untersucht werden.

Bauteile unter dem Einfluss sich drehender Hauptspannungen (multiaxiale Beanspruchung)
Die Berechnung von Bauteilen, bei denen sich die Hauptspannungsrichtungen drehen, ist wesentlich aufwendiger als die Berechnung von Bauteilen, bei denen sich die Hauptspannungsrichtung nicht ändert. Dieser als multiaxiales Problem bezeichnete Fall weist in der Regel eine größere Anzahl von äußeren Belastungen auf, mindestens jedoch 2 äußere Belastungen, z.B. eine Welle unter Torsion und Biegung.
Häufig treten aber auch Dutzende oder gar Hunderte von unabhängigen Belastungen auf, die meist durch gemessene Zeitsignale definiert sind. Solche Problemstellungen finden sich in verschiedenen Bereichen des Maschinenbaus, wie z.B. bei Fahrzeugkarosserien, Achskomponenten, Kurbelwellen, rotierenden Naben in Windkraftanlagen, etc.
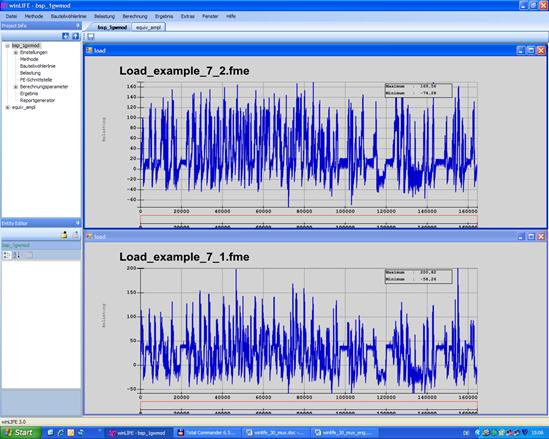
Die folgende Abbildung zeigt das Beispiel eines dynamisch belasteten Achslenkers. Er wird durch eine horizontale und eine vertikale Kraftgruppe F1 und F2 belastet. Da die Kraftgruppen nicht proportional zueinander sind, kann es zu einer Änderung der Hauptspannungsrichtung kommen (multiaxiales Problem).

Bei multiaxialen Problemen ist die Rechenzeit um ein Vielfaches höher als bei uniaxialen oder biaxialen Problemen. Daher werden nur die Knoten auf der Oberfläche betrachtet. Da ein Schaden normalerweise von der Oberfläche ausgeht, stellt diese Einschränkung keine Begrenzung der Lösbarkeit dar. Da auf der Oberfläche ein ebener Spannungszustand vorliegt, wird die Berechnung dadurch weiter vereinfacht.

Die Hauptspannungen als Funktion der Zeit entscheiden darüber, ob ein multiaxiales Problem vorliegt oder nicht. Wenn der Winkel f oder das Verhältnis der beiden Hauptspannungen s2/s1 über der Zeit veränderlich ist, handelt es sich um einen multiaxialen Fall. Dies kann mit Hilfe des Mohrschen Kreises dargestellt werden.
Wenn die Änderung der Hauptspannungsrichtung nicht sehr groß ist, können multiaxiale Probleme zur Vereinfachung ohne Nachteile auch als biaxiale/uniaxiale Probleme behandelt werden. Dies ist für die Berechnung interessant, da Rechenzeit eingespart wird, aber auch für Prüfstandsversuche wichtig, wenn statt vieler Prüfzylinder ein einziger mit nahezu gleichem Schädigungsergebnis verwendet werden kann.
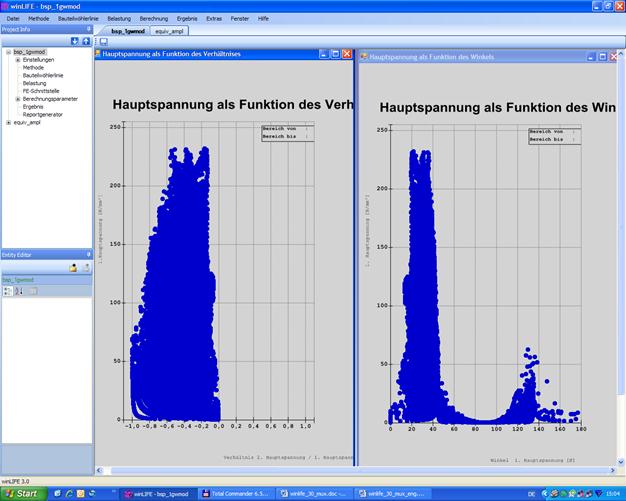
Es ist daher wichtig, den Grad des multiaxialen Problems zu beurteilen, was an Hand der Grafik im folgenden Bild geschieht. Dazu werden der Winkel f und das Hauptspannungsverhältnis s2/s1 für charakteristische Zeitschritte durch je einen Punkt dargestellt (wenn die Punktmenge eine nahezu senkrechte Linie darstellt, liegt kein multiaxiales Problem vor).
Schadensparameter
Da sich der Spannungszustand in der Schnittebene aus Normal- und Schubspannung zusammensetzt, muss daraus eine schädigungsäquivalente Größe ermittelt werden. Folgende Vergleichsspannungshypothesen bzw. Schädigungsparameter sind möglich:
- Normalspannungs - , Schubspannungs und mod. Gestaltänderungsenergiehypothese,
- Findley
- Smith Watson Topper, P. Bergmann, Socie und Fatemi Socie
Richtungsabhängige Lebensdauerberechnung / Nahtschweißverbindungen
Insbesondere in der Windenergie und im Schiffbau sind Strukturspannungskonzepte üblich, da die sehr großen Bauteile anders kaum berechnet werden können. In winLIFE wurden nun mehrere Varianten von Strukturspannungskonzepten integriert. Dazu werden die auf die Schweißnaht extrapolierten Spannungstensoren und die Einheitsnormalvektoren in einer Eingabedatei benötigt.
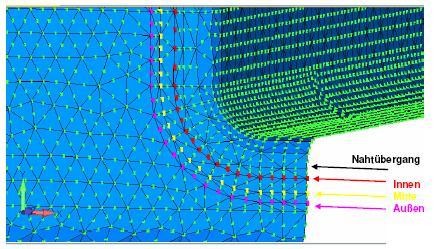
Für die FE-Modellierung müssen bestimmte Regeln angewendet werden. In winLIFE sind verschiedene Verfahren nach GL, IIW, Marquis Bäckström implementiert.
Ablauf einer Lebensdauerberechnung
EINHEITSLASTFÄLLE AUS FINITEN ELEMENTEN, SKALIERT MIT LASTZEITVERLÄUFEN
Die Berechnung läuft - etwas vereinfacht dargestellt – wie folgt ab:
- Im ersten Schritt werden ein oder mehrere FEM-Einheitslastfälle berechnet.
- Eine Material-Wöhlerlinie muss vorliegen oder aber erzeugt werden. Spannungs-Wöhlerlinie oder eine Dehnungs-Wöhlerlinie sein.
- Der Zeitbedarf für eine Berechnung kann erheblich reduziert werden, wenn eine Beschränkung auf ausgewählte Knoten erfolgt. winLIFE bietet die Möglichkeit einer Vorauswahl der zu berechnenden Knoten. Der Anwender kann aber auch individuell die von ihm als kritisch erkannten Knoten auswählen.
- Durch die Verwendung einer Hysterese kann eine erhebliche Rechenzeitverkürzung erreicht werden.
- Für jeden ausgewählten Knoten und Zeitschritt wird der Spannungs-Tensor der elastischen Spannungen berechnet. Dies geschieht durch Skalierung der Einheitslastfälle mit den vorgegebenen Lasten.
- Für eine Anzahl von - je nach Vorgabe des Anwenders - in der Regel 20 Schnittebenen wird eine Spannungszerlegung durchgeführt und eine Schub- und Normalspannung ermittelt. Für diese Ebenen wird dann jeweils eine Schädigung berechnet, für die verschiedene Annahmen getroffen werden können. Die Schnittebene mit der größten Schädigung ist die kritische.

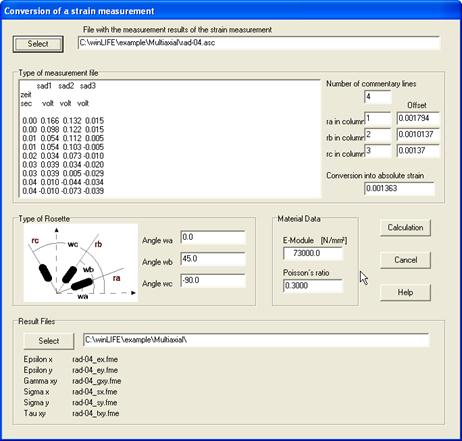
Verwendung von Dehnmessstreifen
Messungen von Dehnmessstreifen können als Grundlage für eine Lebensdauerberechnung dienen. Die Daten der häufig verwendeten Rosetten können direkt eingelesen werden. Das Einleseprogramm ist so flexibel, dass beliebige Rosettenformen und auch sehr unterschiedliche Datenstrukturen eingelesen werden können. Eine Lebensdauerberechnung kann dann für den Punkt des Messortes durchgeführt werden bzw. es ist oft möglich, die gemessenen Daten auf einen anderen Punkt umzurechnen. Dies ist oft notwendig, da an kritischen Stellen oft keine Messungen durchgeführt werden können.
Modale Superposition
Ist bei dynamisch belasteten Bauteilen die Erregerfrequenz der Anregung größer als 1/3 der unteren Eigenfrequenz des Bauteils, so ist die Superposition und Skalierung von statischen Einheitslastfällen nicht mehr zulässig, da die sich einstellenden Schwingungsamplituden nicht einfach linear skaliert werden können. Stattdessen muss das anregende Signal (z.B. mit Hilfe der Fourier-Transformation) in die Signalanteile zerlegt werden, in denen die Eigenfrequenzen vorliegen. Für jede Eigenfrequenz wird der Spannungszustand der Struktur bestimmt.
Bei der modalen Superposition werden dazu zwei charakteristische Größen ermittelt:
- Die Eigenfrequenzen und der zu jeder Eigenfrequenz zugehörige Spannungstensor
- Die modalen Koordinaten stellen die Wichtungsfaktoren dar, mit denen der bei der Eigenfrequenz wirkende Signalanteil multipliziert werden muss.
Formal ist das Verfahren identisch mit der statischen Superposition.
Maßnahmen zur Reduzierung der Rechenzeit
Wenn Last-Zeit-Funktion lang ist, kann die Rechenzeit bei multiaxialen Problemen beträchtlich sein, und die folgenden Maßnahmen wurden ergriffen, um die Rechenzeit zu verkürzen. So wird nicht jeder Zeitschritt der gegebenen Last-Zeit-Funktion berücksichtigt, sondern nur die Zeitschritte, in denen mindestens eine der Last-Zeit-Funktionen einen Umkehrpunkt hat. Weiterhin kann eine Hysterese vorgegeben werden, die zu einer Reduktion der Umkehrpunkte führt.
Diese Maßnahmen führen zu einer starken Reduzierung der Rechenzeit, allerdings auf Kosten der Rechengenauigkeit. Es wird daher grundsätzlich empfohlen, einen ersten Rechenschritt mit den oben genannten Maßnahmen für alle Knoten auf der Oberfläche durchzuführen und dabei eine Liste der Knoten auf der Oberfläche in der Reihenfolge ihrer Schädigung zu erzeugen.
In einem zweiten Schritt wird dann ohne die Maßnahmen zur Rechenzeitverkürzung gerechnet, wobei dann nur noch eine vom Anwender wählbare Anzahl von Knoten – z.B. 100 – berechnet wird, die dann aus der Knotenliste entnommen werden. In diesem Fall werden dann z.B. die 100 Knoten mit der größten Schädigung ohne Vereinfachungen möglichst genau berechnet.
Dieses Vorgehen stellt sicher, dass alle Knoten untersucht werden und dass für die kritischen Knoten die maximal mögliche Rechengenauigkeit verwendet wird.
Analyse der Ergebnisse
In einem multiaxialen Fall ist die Analyse der Ergebnisse besonders wichtig und wird auf folgende Weise ermöglicht: Der Mohrsche Kreis kann für jeden einzelnen Zeitschritt und als Summenbild für alle Zeitschritte und für jede Schnittebene für jeden berechneten Knoten dargestellt werden. Ebenso können die Hauptspannungsvektoren für jeden einzelnen Zeitschritt und als Summenbild für alle Zeitschritte dargestellt werden.
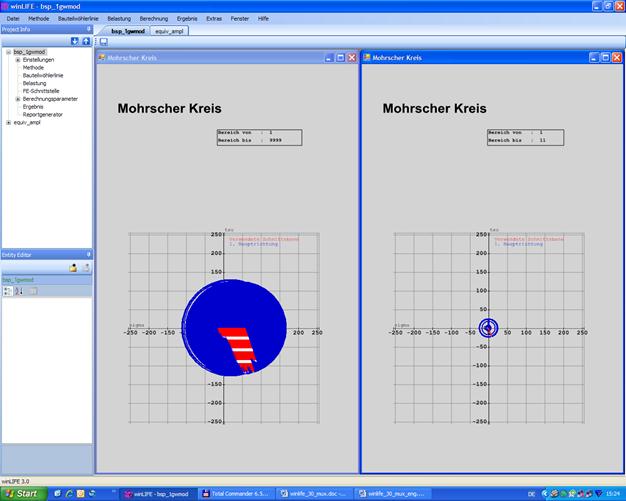
Darüber hinaus kann der Postprozessor des FE-Programms die von winLIFE berechneten Schadenssummen als Farbflächen darstellen.
Da die Vorhersagegenauigkeit für den multiaxialen Fall schlechter ist als für den uniaxialen/biaxialen Fall, ist es wichtig, den Grad der Multiaxialität zu kennen, was mit Hilfe der zuvor genannten Analysetools möglich ist.
Wenn sich herausstellt, dass die Änderung der Hauptspannungsrichtung gering ist, kann der Einfachheit halber auch uniaxial/biaxial gerechnet werden.
Teillastanalyse
Wirken mehrere Lasten auf ein Bauteil, so ist oft von Interesse, welchen Einfluss die einzelne Last auf die Schadenssumme hat. Dies ist mit Hilfe der Teillastanalyse möglich.
Es werden die folgenden drei Varianten untersucht (zur Kennzeichnung der Varianten werden die aus der Mengenlehre bekannten Symbole verwendet):
- ∃! (= Es existiert nur Eine (Last) ): nur eine der existierenden Lasten wird berücksichtigt, die anderen werden alle auf Null gesetzt.
- -∃! (=Genau Eine (Last) existiert nicht):es wird eine aller wirkenden Lasten = 0 gesetzt, die restlichen Lasten bleiben unverändert.
- ∀∃ (beliebig): es können vom Benutzer beliebige Kombinationen gewählt werden.
Für jede existierende Last-Zeit-Funktion wird eine Spalte L1, L2, .. erzeugt, in der der Multiplikator angegeben ist. Ist dieser =1, wird die Last-Zeit-Funktion unverändert verwendet, ist er =0, wo wird diese =0 gesetzt.
Die Spalte Index entspricht der Zeilennummer in der Matrix.
Die aus der Mengenlehre bekannten Symbole bedeuten:
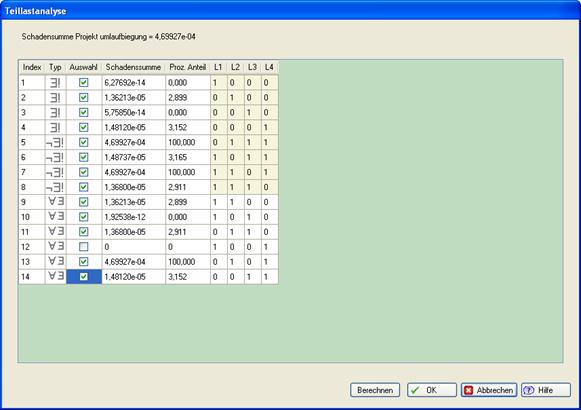
Die Eingaben in der obigen Maske haben folgende Bedeutung:
Zeile 1: Last 1 wirkt, die übrigen Lasten sind = 0.
Zeile 2: Last 2 wirkt, die übrigen Lasten sind = 0.
Zeile 3: Last 3 wirkt, die übrigen Lasten sind = 0.
Zeile 4: Last 4 wirkt, die übrigen Lasten sind = 0.
Zeile 5: Last 1 wirkt nicht, die übrigen Lasten sind unverändert.
Zeile 6: Last 2 wirkt nicht, die übrigen Lasten sind unverändert.
Zeile 7: Last 3 wirkt nicht, die übrigen Lasten sind unverändert.
Zeile 8: Last 4 wirkt nicht, die übrigen Lasten sind unverändert.
Zeile 9: Last 1 und 2 wirken, die übrigen Lasten wirken nicht.
Zeile 10: Last 1 und 3 wirken, die übrigen Lasten wirken nicht.
Zeile 11: Last 2 und 2 wirken, die übrigen Lasten wirken nicht.
Zeile 12: Last 1 und 4 wirken, die übrigen Lasten wirken nicht.
Zeile 13: Last 2 und 4 wirken, die übrigen Lasten wirken nicht.
Bild 1: Last 3 und 4 wirken, die übrigen Lasten wirken nicht.
Rotierende Lasten
Der Fall rotierender Lasten wird behandelt, indem die gegebene(n) Belastung(en) in mehrere statisch äquivalente Einzellasten aufgeteilt wird (werden). Jeder dieser Einzellasten wird ein Winkelfenster zugeordnet, in dem sie wirkt.
In Verbindung mit den jedem Winkelfenster zugeordneten Einzellastfällen kann die Rotation eines Bauteils durch statische Überlagerung korrekt behandelt werden.