CRACKGROWTH
In vielen Bereichen der Technik erfolgt eine Auslegung bis zum technischen Anriss (Risslänge ca. 0,1 bis max. 1 mm) und eine weitere Nutzung des Bauteils nach diesem Anriss sollte nicht mehr erfolgen. Der Grund dafür ist, dass die Zyklenzahl zwischen dem ersten Anriss und dem vollständigen Versagen des Bauteils in der Regel sehr kurz ist (ca. 5 bis 10 % der Gesamtlebensdauer), so dass eine weitere Verwendung schon wegen des ungünstigen Nutzen-Risiko-Verhältnisses nicht sinnvoll ist.
Auch wenn die Verwendung eines Bauteils mit Anriss nicht vorgesehen ist, stellt sich bei sicherheitsrelevanten Bauteilen häufig die Frage, ob die Funktion und die Tragfähigkeit auch im angerissenen Zustand noch gegeben ist und welche Restlebensdauer noch vorhanden ist. Diese Beurteilung dient dann insbesondere der Absicherung der Lebensdauer beim Auftreten von Fehlstellen, die durch zerstörungsfreie Prüfung nicht mit Sicherheit gefunden werden können [5].
Anders verhält es sich in der Luft- und Raumfahrt, wo Leichtbaukonstruktionen aus Aluminiumlegierungen eingesetzt werden. Hier ist die Zyklenzahl zwischen dem ersten Anriss und dem Versagen deutlich höher, so dass der Einsatz von Bauteilen mit Rissen üblich und vertretbar ist. Allerdings muss die Phase des Risswachstums gut bekannt sein, und es muss sichergestellt sein, dass die Risse bei der Inspektion gefunden werden, bevor das Bauteil versagt. Eine Rissfortschrittsanalyse ist daher eine wichtige Maßnahme zur Festlegung der Inspektionsintervalle.
Auch bei der Analyse und Rekonstruktion von Schäden ist es oft wichtig, das Risswachstum abschätzen zu können, so dass sich auch Schadensgutachter mit diesem Thema beschäftigen müssen.
In winLIFE werden wenige, aber für eine Abschätzung ausreichende Methoden zur Rissfortschrittsberechnung zur Verfügung gestellt, so dass eine hilfreiche Ergänzung zu den Berechnungsmethoden bis zum Anriss gegeben ist.
Linearelastische Bruchmechanik (LEBM)
Die linear elastische Bruchmechanik (LEBM) wird bei vollständig oder nahezu sprödem Werkstoffverhalten angewendet.
Ziel ist die Vorhersage des Rissfortschritts mit Hilfe von Nennspannungen. Eine wichtige Kenngröße für den Rissfortschritt ist der Spannungsintensitätsfaktor K (SIF = Stress Intensity Factor). Er ist ein Maß für die Intensität des Spannungsfeldes an der Rissspitze und hängt ab von
- der Geometrie des Bauteils
- der Rissgröße
- und der Beanspruchung
Der Spannungsintensitätsfaktor wird nach folgender Beziehung ermittelt:
K = σ * (π a) (1/2) Y

Die Grafik zeigt, dass sowohl die Geometrie - konkret das Verhältnis von Höhe zu Breite - als auch die Risslänge von Bedeutung sind. Arbeitet man nach dem hier beschriebenen Verfahren und verwendet die Bruttonennspannungen als Grundlage, so ist für jede Querschnittsform der Verlauf des Korrekturfaktors von Bedeutung. Für eine Vielzahl von Geometrien liegen Korrekturfunktionen vor. Wenn ein reales Bauteil vorhanden ist, wird versucht, ein ähnliches Bauteil aus der Bibliothek als Referenz zu verwenden. Ist dies nicht möglich, muss mit Hilfe der FEM vorgegangen werden.
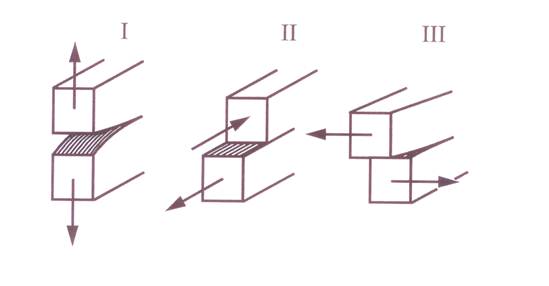
Das Risswachstum wird durch das Spannungsfeld in der Umgebung der Rissspitze verursacht. Von den drei Beanspruchungsarten von Rissen dominiert der sogenannte Mode I, der in den meisten Fällen für den Rissfortschritt relevant ist. Dieser Fall ist in winLIFE implementiert, die beiden anderen, relativ seltenen Modi II und III sind (zunächst) nicht berücksichtigt, werden aber in einer späteren Version implementiert.
Zur Berechnung des Rissfortschritts wird im einfachsten Fall die Gleichung nach Paris verwendet:
da/dN = C (ΔK)m
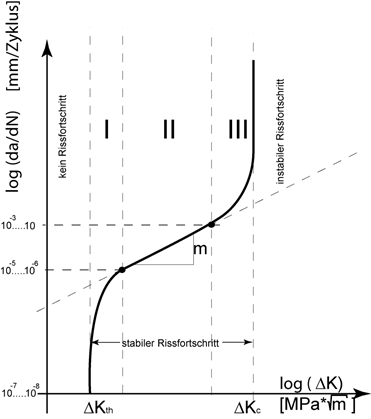
Diese gilt für das Intervall.
ΔKth< ΔK < ΔKC
Dabei bedeuten:
da = Änderung der Risslänge [mm]
dN = Änderung der Zyklenzah [1]
C = Materialkennwert für das Einheitensystem: Nmm-3/2
Ist C für das Einheitensystem MPa m1/2 gegeben, muss C mit dem Faktor 0,031623m multipliziert werden, um im Einheitensystem von winLIFE rechnen zu können.
m = Steigung [1]
ΔKth = Grenze, unterhalb der kein Rissfortschritt stattfindet [Nmm-3/2]
Ist ΔKth in der Einheit MPa m1/2 gegeben, muss dieser Wert mit 31,623 multipliziert werden, um die Einheit Nmm-3/2 zu erhalten.
ΔKC= Grenze, oberhalb der instabiler Rissfortschritt stattfindet [Nmm-3/2 ]
Ist ΔKC in der Einheit MPa m1/2 gegeben, muss dieser Wert mit 31,623 multipliziert werden, um die Einheit Nmm-3/2 zu erhalten.
Die Paris-Gleichung gilt nur im Interval 2 und bezieht auch nicht das Spannungsverhältnis RK mit ein. Abhilfe schafft hier ein Ansatz von Erdogan-Ratwani, der für alle drei Bereiche gilt:
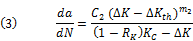
Dabei bedeuten:
da = Änderung der Risslänge [mm]
dN = Änderung der Zyklenzahl [1]
C2 = Materialkennwert
m2 = Steigung [1]
ΔΚth = Grenze unterhalb der kein Rissfortschritt stattfindet [Nmm-3/2 ]
ΔΚc = Grenze oberhalb der instabiler Rissfortschritt stattfindet [Nmm-3/2 ]
RK = Spannungsintensitätsfaktorverhältnis Kmin/Kmax [1]
Die Berechnung des Rissfortschritts erfolgt nach der Paris-Gleichung in folgender Reihenfolge:
- Datenvorgabe: Werkstoffkonstanten Co und m.
- Anfangsrisslänge ao
- Anfangslastspielzahl No Diese hat keinen Einfluss auf den berechneten Rissfortschritt, wird aber oft benötigt, wenn die Lastgeschichte der Vergangenheit berücksichtigt werden soll. In den meisten Fällen wird jedoch mit No=0 gearbeitet.
- Korrekturfunktion Y(a): Die Korrekturfunktion berücksichtigt die Geometrie und die Risslänge. Bei Änderung der Risslänge a ändert sich auch die Korrekturfunktion. Nur bei kurzen Intervallen kann die Korrekturfunktion konstant gehalten werden.
- Rissfortschritt: Der Rissfortschritt dl wird nach Gleichung 3 bestimmt. Es ist zu beachten, dass die Längenänderung des Risses zu einer Änderung der Spannungsintensität K und der Korrekturfunktion Y führt. Die Reihenfolge der Beanspruchung ist daher von großer Bedeutung.
Die Berechnung nach dem Ansatz von Erdogan-Ratwani erfolgt in ähnlicher Weise.