CRACKGROWTH
In many areas of engineering, a design is made up to the technical crack (crack length approx. 0.1 to max. 1 mm) and further use of the component after this crack should not take place. The reason for this is that the number of cycles between the first crack and the complete failure of the component is usually very short (approx. 5 to 10% of the total fatigue life), so that further use is not advisable due to the unfavourable risk/benefit ratio.
Even if the use of a component with a crack is not intended, the question often arises in the case of safety-relevant components as to whether the function and load-bearing capacity is still given in the cracked state and what remaining fatigue life is still available. This assessment then serves in particular to safeguard the fatigue life in the event of defects that cannot be found with certainty by non-destructive testing [5].
IThe situation is different in the aerospace industry, where lightweight aluminium alloy structures are used. Here the number of cycles between the first crack and failure is significantly higher, so the use of cracked components is common and justified. However, the crack growth phase must be well understood and it must be ensured that the cracks are found during inspection before the component fails. Crack growth analysis is therefore an important means of determining inspection intervals.
It is also often important to be able to estimate crack growth when analysing and reconstructing damage, so damage assessors also have to deal with this issue.
winLIFE provides a small number of crack propagation calculation methods that are sufficient to estimate crack propagation, thus providing a useful supplement to the calculation methods up to crack initiation.
Linear Elastic Fracture Mechanics
Linear elastic fracture mechanics is used for materials that are completely or almost brittle.
The aim is to predict crack propagation using nominal stresses. An important parameter for crack propagation is the stress intensity factor (SIF). It is a measure of the intensity of the stress field at the crack tip and depends on:
- the geometry of the component
- the crack size
- the stress
The stress intensity factor is determined by the following formula:
K = σ * (π a) (1/2) Y
The graph shows that both the geometry - specifically the ratio of height to width - and the crack length are important. When working with the method described here and using gross nominal stresses as a basis, the course of the correction factor is important for each cross-section shape. Correction functions are available for a large number of geometries. If a real component is available, an attempt is made to use a similar component from the library as a reference. If this is not possible, the FEM must be used.
Crack growth is caused by the stress field near the crack tip. Mode I, most relevant to crack propagation, dominates among the three types of crack-related stresses. This case is implemented in winLIFE, the other two relatively rare modes II and III are not (yet) considered, but will be implemented in a later version.

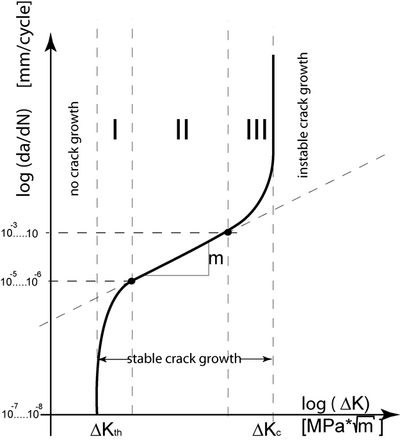
In the simplest case, the Paris equation is used to calculate the crack propagation: da/dN = C (ΔK)m
This applies to the interval ΔKTH<ΔK < ΔKC
Whereby:
da =change in crack length [mm]
dN = change in number of cycles [1]
C = material property value for the unit system Nmm-3/2
If C is given for the unit MPa m1/2, C must be multiplied by the factor 0.031623m to be able to calculate in the unit system of winLIFE.
m = slope [1]
ΔΚth= limit below which no crack propagation occurs [Nmm-3/2]
If ![]() is given in the unit MPa m1/2, this value must be multiplied by 31,623 to obtain the unit Nmm-3/2.
is given in the unit MPa m1/2, this value must be multiplied by 31,623 to obtain the unit Nmm-3/2.
ΔΚC= above which unstable crack propagation occurs [Nmm-3/2]
If ![]() is given in the unit MPa m1/2, this value must be multiplied by 31,623 to obtain the unit Nmm-3/2 .
is given in the unit MPa m1/2, this value must be multiplied by 31,623 to obtain the unit Nmm-3/2 .
The Paris equation applies only to interval 2 and does not include the stress ratio RK. The Erdogan-Ratwani approach, which applies to all three areas, provides a remedy here:

Whereby:
da = alteration of the crack length [mm]
dN = alteration of the number of cycles [1]
C2 = material characteristic
m2 = slope [1]
ΔΚth = limit below which there is no crack propagation [MPa m1/2]
ΔΚc = limit above which the crack propagation is instable [MPa m1/2]
RK = stress intensity factor ratio Kmin/Kmax [1]
The steps for calculating the crack propagation with the Paris equation are as follows:
- Data specification: Material constant Co and m.
- Initial crack length ao
- Initial number of cycles No
This has no influence on the calculated crack propagation, but is often required if the load history of the past is to be taken into account. In most cases, however, No=0 is used. - Correction function Y(a):
The correction function takes into account the geometry and the crack length. If the crack length a changes, the correction function also changes. The correction function can only be kept constant for short intervals. - Crack propagation:
The crack propagation dl is determined according to equation 3. Note that as the crack length changes, the stress intensity K and the correction function Y change. The order of stressing is therefore of great importance.
The calculation according to the Erdogan-Ratwani approach is carried out in a similar way.